20年ぶりの言葉たち
久しぶりに参考書を開くと、登場するのは「同位角」「錯覚」「相似」「合同」「三平方の定理」「中点連結定理」……などなど。普段は使わない言葉たち。特に最後の「中点連結定理」に至っては高校受験以降いちども頭の引出しを開けていなかったようで、名前を見た瞬間に、蒸し暑い通学路の風景がフラッシュバックした。
死蔵されているこの知識。なんとかして生かせないだろうか。
そう思って、こんなものを買ってきた。

おいしいりんごのタルトです
図形には三角形の問題がやたら出てくるのだが、日常で三角形を扱う機会がない。ホールから切り出したこれなら、二等辺三角形だ。(本当は一辺が弧だけど、そこはまあ…)

お店の名前も図形っぽい、「45度」
たとえば、これを使って図形の問題を再現してみよう。

一見、ただのタルトとポッキーですが
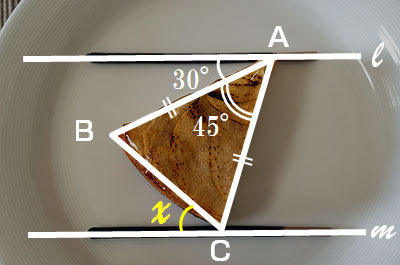
測ったらタルトが本当に45度で切られていて見事だった
肩慣らしとして、これを解いてみよう。出題は、「xの角度を求めよ」。
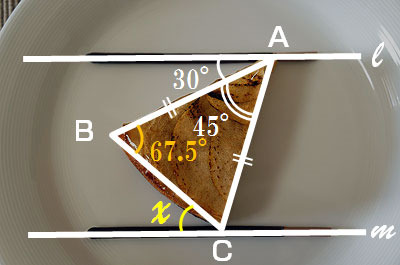
三角形の内角の和は180度。かつタルトは二等辺三角形なので、角ABCは (180度-45度)/2 = 67.5度
ここで、唐突にポッキーがもう1本登場する。数学でよくでてきた「補助線」というやつである。

実際おいてみるとあんまり見たことのない状況だ
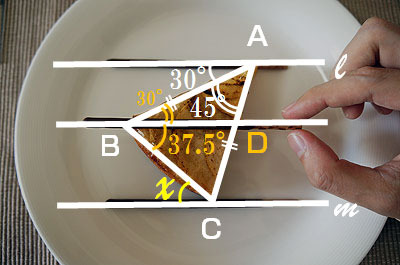
各ABDは上の30度と錯角になる。錯角は等しいためこちらも30度。すると各DBCは、さっき求めた67.5度-30度 = 37.5度。これが角xと錯角なので、角x=37.5度!
タルトの下、角xは37.5度であった。
これまで「概念」としてしか扱ってこなかった図形、それがケーキとポッキーになることで、だいぶ実生活に近づいてきた。
ただ、これではあくまで、数学の問題をモノに置き換えただけだ。僕はもっとこう、生活の中で困ったことを、図形を使って解決したりしたいのだ。
応用例1・長い直線を引く

あー困った、困った……

直線が引きたいのに全然うまく引けないよ~~

定規を使えばいいんだけど、手元には三角形をしたアボカドチップスしかないし。どうしよう。

こうやってチップスのふちを使えば……

だめだ……、これじゃ短すぎるよー。困った~~

そうだ、中学校で習った図形の知識を使えばいいんだ!!

内角の和が180度ということはつまり、

こうすれば継ぎ目が180度になって、チップスのふちに長い直線ができる!

いやまてよ……。確かにひとつの三角形の内角の和は180度。でももし、一つ一つのチップスの形がちがっているとしたら、これでは180度にはならない……

そうだ!
図形の知識②
<三角形の合同条件>
一組の辺とその両端の角がそれぞれ等しい

重ねて比較。この一辺の長さは3枚とも等しい。

その両端の角は、すべて70度。3枚のチップスの形はすべて合同、短辺の両側の角が70度の二等辺三角形だ。

ということは内角の和は180度。この2枚のチップスのふちはたしかに直線だ!

やった!長い直線が引けちゃった!
どうだろう、こういうサクセスストーリー。
直線を引きたいけど定規がない、という状況は日常生活の中で割とある。そんな時、図形の知識があれば手近にあるものを使って(それがアボカドチップスである機会は少ないかもしれないが)直線がズバッと引けてしまうのだ。図形、習っててよかった!

引けた長い直線
応用例2・頭のサイズを測る

……
ここは渋谷ヒカリエの廊下。従業員出入り口脇の角である。ここに一人の男性が体操座りをしているのだが、いったい彼は何をしているのか、おわかりだろうか。
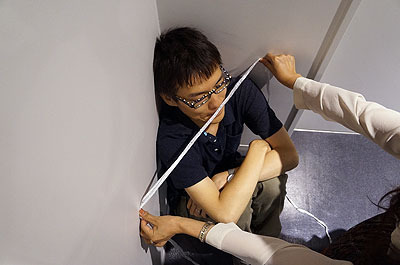
そこへおもむろに1本のロープが
何が起きているのか、読者の皆さんにはまだ呑み込めていないことと思う。
では、こうしてみたらどうだろうか。
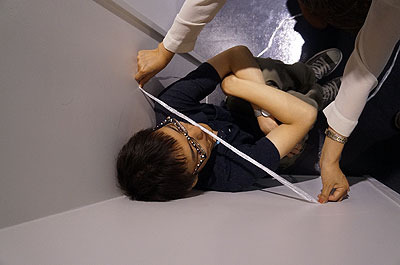
お分かりいただけただろうか
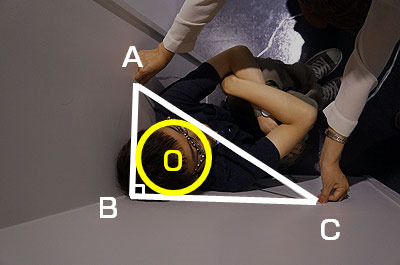
これは図形の問題である
直角三角形ABCと、それに内接する円Oがある。
このとき、円Oの円周を求めよ。
そう、実は頭囲を測っているのだ。三平方の定理の応用問題である。
これだけでは情報が足りないので、二辺の長さを測ってみよう。

辺ABは30cm

辺BCは48cmであった。
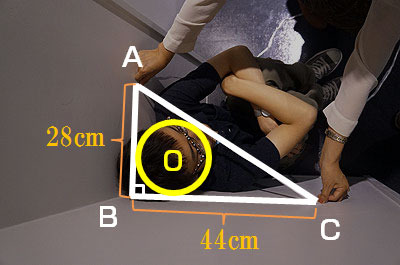
円Oの円周を求めよ。
(解法)
三平方の定理より、
AC^2 = 28^2 + 44^2
AC = 52.2 cm
円Oの中心点Oを使って三角形ABCを3分割する。
三角形ABC = 三角形OAB + 三角形OBC + 三角形OCA
円Oの半径をxとして、三角形の面積の公式に当てはめる。
44*28/2 = 28x/2 + 44x/2 + 52.2x/2
616 = 62.1x
x = 9.9cm
円周を求める
9.9 * 2 * 3.14 = 62.2 cm
わかった。
この男性、まあ筆者なんだが、僕の頭のサイズは62.2cmであることがわかった。

なんかちょっと大きい気がするがどうなんだろう……
さて、正確さの問題はさておき、この事例には重大な欠陥がある。
この問題には別解があるのだ。「ロープを頭に巻いて一周の長さに目印をつけておき、あとでロープを伸ばして定規で測る」である。
うう、明らかに別解の方が手軽かつシンプルだ。
図形の知識を生かしたいあまり、ずいぶん頭でっかちな回答をしてしまった。(頭囲だけに)
応用例3・不良の開脚度を調べる
このページで挑戦は最後となる。たとえば、街を歩いていてこんな場面に出くわしたとしよう。

あっ、不良だ!
不良がいる。しかもこっちをにらんでいる。怖い!
しかし堂に入ったヤンキー座りだな。足がすごくよく開いているぞ。あれ、何度くらいあるんだろう。
気になってきた……。

分度器を当てて測ってみよう

「何やってんだコラ」

「オレは開脚角度を分度器で測られるのが一番ムカつくんだよ!」
こうなることは予想に難くない。
では、いったいどうしたら、不良の開脚角度を知ることができるだろうか。

これを使います

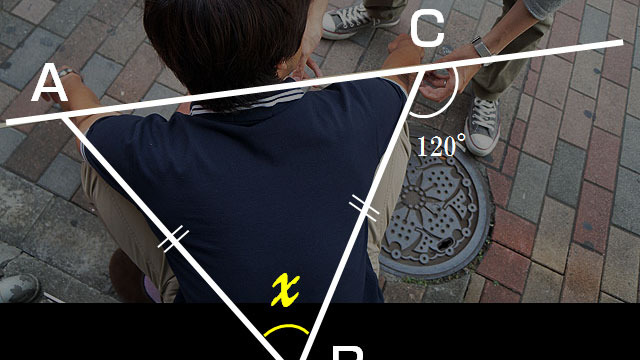
不良の両膝の先端を通る補助線を引く

こうすることにより、ここに二等辺三角形ができる(両足の長さはほぼ同じとする)

ちなみに補助線と足のつくる角は120度
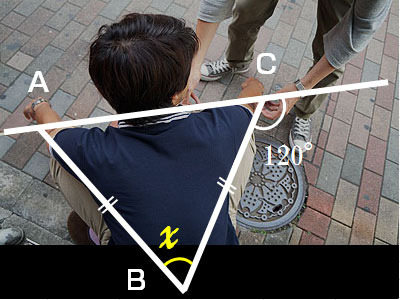
図形の問題にするとこうなる
(解法)
角ACBは 180度 - 120度 = 60度
二等辺三角形なので角BACも60度
三角形の内角の合計は180度なので、角ABCをxとすると
x = 180度 - (60度 + 60度)
x = 60度
つまり、不良の開脚角度は60度である。偶然にも正三角形であることが判明した。一見、柄の悪く見える姿勢だが、幾何学的にはかなりの「いい姿勢」だったのである。
そんな事実が明らかになった今でも、不良はまさか自分の開脚角度が測られたなんて夢にも思っていないはずだ。だって実際に測ったのは、あくまで補助線と足の角度なのだから。
また、不良に接近するのが恐ろしい場合、こういった応用もできる。

先ほどの補助線を延長し、少し離れたところに不良の片足と平行な補助線をもう一本引く。

足と補助線は平行なため、ここは同位角となる。同位角は等しいため、角bの角度を測れば、先ほど同様、開脚度を計算できる。
中学数学の知識さえあれば、不良に触れずにその開脚角度を知ることすら可能。
日本の義務教育のレベルの高さを思い知った瞬間であった。
もうちょっとある気もする
「日常生活に応用する」と言いつつ、日常生活でそんなことあるか!という例ばかりになってしまった。
当初はけっこう真面目な企画だったのだが、高校入試の過去問を入手し、問題を現実で再現しようとがんばった結果、こうなってしまったのだ。
その後ひとにきいたりネットで調べたりしたところ、図形の知識の活用としてこんな例があるそうだ。
・影の長さから建物の高さを知る
・変な形の農地を平等に分ける
・丸太から角材を切り出す時の寸法を計算する
などなど。どれも日常生活と言い切るにはちょっとレアなシーンである。
しかし予期せぬことが起こるのが人生。日常といってもよく見ればレアなシーンの連続だ。
今後、図形問題を生かせるタイプのレアなシーンはやってくるのか。その到来を楽しみにしつつ、これからも日常を過ごしていきたい。