社会の歯車
3Dプリンタでいろんな歯数の歯車を試しているうちに、歯車の仕組みが分かってきた。そんな自分も気づけば社会の歯車である。潤滑油のほどよく効いた忖度歯車だ。せめて歯数は素数だといいな。


3Dプリンタを買ったら、なんでも自分で作れることに気がついた。今回はスピログラフっぽいものを作る。穴の開いた定規に円盤できれいな模様を描くやつだ。3Dプリンタがあれば作り放題だ。たくさん作ったので見てほしい。
スピログラフという名前にはあまりなじみがないかもしれないが、写真を見てもらったら伝わると思う。

ダイソーではくるりんデザイン定規として売られている。調べてみるとスピログラフはハズブロ社によって商標登録されており、商品名に使えないようだ。なのでこの記事でも「スピログラフっぽいもの」ということにする。
仕組みは簡単だ。穴の内側にギザギザがついており、円盤の外側にもギザギザがついている。そして、円盤の穴にペンをさしこんで穴にそって動かすと、歯車の原理で円盤が穴の内側を回る。これにより、予測できそうでできない、なんかいい感じのきれいな模様が描ける。
僕がこれに出会ったのは保育園に入った時だったと思う。今から20年以上前だ。でも、あんまりうまくできなかった記憶がある。力を加える方向を間違えるとすぐに歯車が外れてしまう。これを未就学児があやつるのはけっこう難しい。

スピログラフっぽいものを3Dプリンタでつくる。といっても、歯車をつくるだけなのでとても簡単である。以前日本列島のモビールを3Dプリンタでつくったときに紹介したFusion 360という3Dモデルソフトには、歯車を簡単に作れる機能がある。



これで模様を描くとどうなるか。48÷16=3なので、3に関係する何らかの模様ができそうだ。やってみないとわからないが、三角形が何個もできるのかな。


できあがりの感動を最大限にするため、あえてあまり調べず、そして深く考えず歯数を設定したのだが、数時間の印刷を経て完成したのはおにぎり描画専用定規だった。そっか。48÷16=3ということは、3回円盤が回転してもとの位置に戻るのか。もとの位置に戻ったらもう同じ線をたどるしかない。ちょっと考えたらわかることだった。
歯数が48の穴に対し、歯数が16の円盤だと三角形っぽい模様になった。これは、48÷16=3によるものだ。
これは面白いぞ。歯数によって模様が変わるのであれば、いろんな歯数の円盤を作ってみたい。僕には3Dプリンタがある。ダイソーのくるりん定規ではためせないような、いろんなパターンを遊び尽くしたい。
歯数を様々に変えた円盤と輪っかを作った。




なんで歯数を60にしたかというと、60はたくさんの約数を持つからである。60は2でも3でも4でも5でも6でも割れる。試しがいがある。
突然ですがここでクイズです。
歯数が60の穴に対し、歯数が30の円盤で模様を書くとどうなると思いますか?
60÷30=2。でも二角形なんて存在しない。二角形ぽいものってなんだろう。いったいどんな模様になっちゃうんだろう。ドキドキしてきた。
正解はこちら。
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓

できたのは楕円だった。ユークリッド幾何において二角形は存在しないが、2つの線がぴたっとくっついた図形だと思えば良さそうだ。そして、さっきの三角形っぽいものが丸みを帯びていたように、2つの線が丸みを帯びると楕円になる。
じゃぁ、歯数が60個の穴に対し、歯数が10、12、15、20の円盤だとそれぞれどうなるでしょうか。たぶん想像つくと思います。

ここまで試したのはいずれも、「穴の歯数の約数」である。そのため、穴のまわりを一周するだけで模様が完成してしまった。しかし、ここから試すのは割り切れない数である。たとえば、歯数が60の穴に対し歯数が18だとどうなるだろう。60÷18=3あまり6。穴のまわりを一周した時点で、円盤の歯が6余分に進んでいることになる。どんな模様になると思いますか。
答えは、こんな感じ。

ちなみに、色をつけると伝わりやすいと思うが、おにぎりっぽいものが3個つながった模様になっている。

さっき、「穴のまわりを一周した時点で、円盤の歯が6余分に進んでいることになる。」と言ったが、18÷6=3なので、穴の周りを3周すると、円盤の余分に進む歯数が18となり、ちょうど円盤一周分となる。すなわち、穴と円盤の周期が一致する。だから三連おにぎりになったわけか。なるほど〜。(自己解決して納得する様子)
同じ考え方で、円盤の歯数を16にしたときのことを考えてみる。60÷16=3あまり12なので、穴のまわりを一周した時点で、円盤の歯が12余分に進んでいることになる。2周だと24。3周だと36。4周目だと48となり、ようやく16の倍数である。つまり、ここで周期が一致する。
できるのはきっと四連おにぎりだ。いや、16は20(三角形っぽいもの)よりも15(四角形っぽいもの)に近いので、四連アルフォートのほうがいいかもしれない。

穴の周りを何周すれば完成するか。歯数が60の穴に対し、歯数が10、12、20、30のときは1周で、18のときは3周、16のときは4周だった。いちいち余りの計算をしていたら大変なので、もっと早く計算したい。なんかいい計算方法はないだろうか。

表にしてみて規則性を見つけてみる。僕が見つけた規則性は、「周数は、穴の歯数と円盤の歯数の最小公倍数を穴の歯数で割った値」というものだ。
例えば、穴の歯数が60で、円盤の歯数が18のとき。18と60の最小公倍数は180。これを穴の歯数60で割ると3だ。これが周数である。最小公倍数がスピログラフで役立つとは。算数勉強しててよかった〜。

さっそく試してみる。穴の歯数が60で、円盤の歯数が14のときはどうなるか。60と14の最小公倍数は420。420÷60=7なので、7周だ。7連アルフォート。

前述の通り、スピログラフを描くときに何周するかは、穴の歯数と円盤の歯数の最小公倍数によって決まる。このとき、穴の歯数と円盤の歯数が「互いに素」だとどうなるか。「互いに素」とは、2つの整数の共通の約数が1しかないということだ。例えば、8と15は互いに素である。
穴の歯数と円盤の歯数が「互いに素」なとき、最小公倍数は「穴の歯数×円盤の歯数」となる。これを穴の歯数で割ると、商は円盤の歯数となる。すなわち、「円盤の歯数」回だけぐるぐる回す必要があるのだ。しんどい。
歯数が11、13、17、19のときは穴の歯数60に対して「互いに素」になるので、それぞれの歯数の分だけぐるぐる回す必要がある。やだなぁ。


円盤のどこにペンを挿すかでも模様は変わる。今回は歯数が59の穴に対し、歯数が30の円盤を利用し、ペンの位置をいろいろ変えてやってみた。



調べてみると、そもそもスピログラフで描かれる曲線はトロコイドというらしい。アンドロイドみたいでかっこいいな。軌跡の数式の話はここにのっている。ちょっと難しいけど、いちおう理系の高校数学の範囲内である。でも今日は頭を空っぽにして歯車を回すので十分だ。
歯数が60の穴に対し、円盤の歯数が20だと楕円、30だとおにぎりになったが、40とか50だとどうなるのだろうか。


自作のスピログラフっぽいものを遊びつくしたところで、ダイソーのくるりん定規にもどる。この歯数を数えてみよう。

「でました。」と言ったが歯数を数えるのはけっこう大変だった。ネットフリックスでインディージョーンズを流しながら数えていたが、数える方にかなりの集中力が必要だったので最後の方のアクションシーンをほとんど観れなかった。

組み合わせによって簡単だったり難しかったりする。こういうのは子供の成長段階に合わせて楽しめるようになっているんだなぁ。とはいえ、歯数を数えない限りやってみないと難易度がわからないけれど。
くるりん定規は、自作のスピログラフっぽいものと比較して、圧倒的に回しやすい。よくみると穴のギザギザの上にカバーがついている。これのおかげで外れにくくなっているのだ。

さて、穴の内側ばかりぐるぐるしてきたが、外側を回すとどうなるだろう。今回は外側にもギザギザを作った。歯数は90である。




なるほど。まぁまぁきれいだけど感動がうすい。コスパが悪いなぁと思った。実は途中で「左右の手の持ち替え」が発生するため、なかなか大変なのである。

最後は直線に沿って円盤を回そうと思う。実は、ギザギザのついた直線も用意していたのである。

ただただゆるやかな波ができるだけだった。いろんな模様を描きすぎてもうお腹一杯になっているので、これぐらいシンプルなぐらいがちょうどいい。なごむねえ。

↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
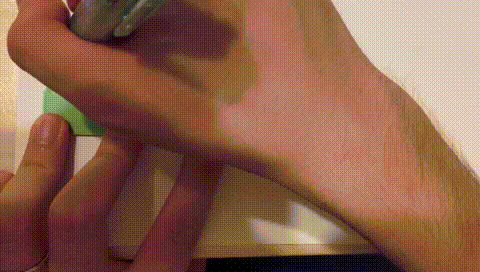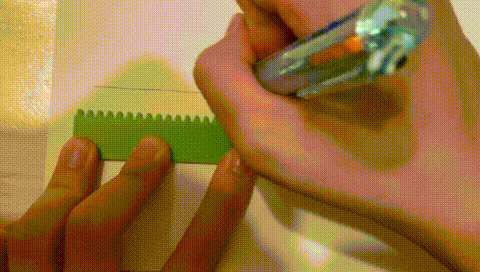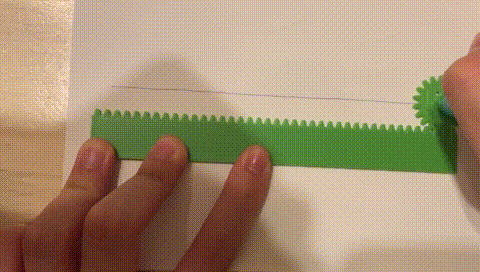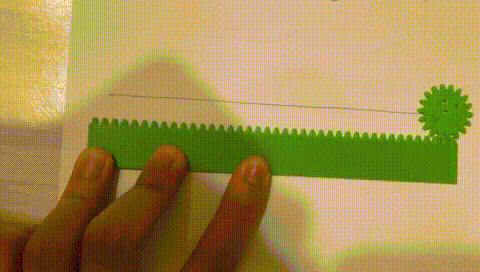

3Dプリンタでいろんな歯数の歯車を試しているうちに、歯車の仕組みが分かってきた。そんな自分も気づけば社会の歯車である。潤滑油のほどよく効いた忖度歯車だ。せめて歯数は素数だといいな。

| ▽デイリーポータルZトップへ | ||
| ▲デイリーポータルZトップへ |