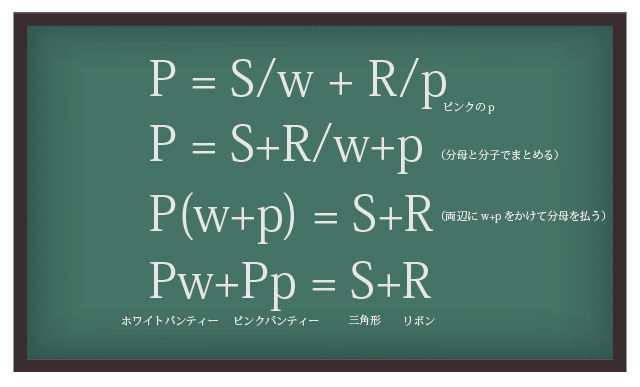三角形の箱が少ない理由
先日のクリスマスでは、誰かにプレゼントをした人も多いと思う。 そのプレゼントは大抵がリボン付きの四角い箱をであることが多いのは、 今回のような理由があるからである。 お店の人たちがうっかりパンティーになってしまうことを事前に防いでいるのだ。
そういった見えない人たちの努力によって、私たちの普通の生活がなりたっていることを忘れてはならない。
そういった見えない人たちの努力によって、私たちの普通の生活がなりたっていることを忘れてはならない。
解けないリボン
これがリボンの付いたパンティーである。
正確にはショーツというそうだ。
しかし今回の企画で必要なのはリボンなので、 それ以外の部分は必要ない。
白、ピンク、黒。
このリボン、いったいどうやって付いているのかと思ったら、 結び目から直接パンティーに縫い付けられていた。
なので布から直接切り取ったが、解けないリボンというのは、一種のパラドックスのような存在である。
なので布から直接切り取ったが、解けないリボンというのは、一種のパラドックスのような存在である。
単体だとオシャレアイテム
これらのリボンはそれだけで なんでもパンティー化させてしまう強烈なアイコンだと冒頭で述べた。
しかし試して気づいたが、リボンだけでそうなるほどではなかった。
しかし試して気づいたが、リボンだけでそうなるほどではなかった。
アメリカンカレッジのダンスパーティーにて。
プレゼントにどうぞ。
どちらも全然パンティーではない。
考えてみればリボン自体は普通にリボンである。 それでパンティーに見えてしまっては世界がとんでもないことになるではないか。
考えてみればリボン自体は普通にリボンである。 それでパンティーに見えてしまっては世界がとんでもないことになるではないか。
要素に分解し方程式で表す
ここは冷静に、リボンとその他の要素を分けて考えてみよう。
リボンのみ。当然リボンにしか見えない。
白い三角のみ。単なる三角以外のなにものでもない。
しかしその二つが合わさると、紛れもない物になる。
なるほど、リボンに三角形を加えるとこうなるらしい。 この関係はこういった簡単な式として表せないだろうか。
つまり三角形であれば、リボンを付けるだけでパンティーになるということ。 また、三角形はパンティーからリボンを抜いた物に等しく、リボンはパンティーから三角形を抜いた物に等しいことも分かる。
本当にこの方程式が正しいのか、 三角形にリボンを足してみて証明してみようと思う。
本当にこの方程式が正しいのか、 三角形にリボンを足してみて証明してみようと思う。
いったん広告です
仮定から証明へ
三角形にリボンを足せばどんなものでも パンティーになる。
この仮定を証明するために、 色々な三角形にリボンを付けて確かめてみよう。
この仮定を証明するために、 色々な三角形にリボンを付けて確かめてみよう。
普通のＡ４紙。
これにリボンを付けてもなんにもならない。
ところが三角形にカットすると、
パンティーになる。
ただの紙も、三角形にしてリボンを付けただけでかなりの意味をもつ物になる。 まるで錬金術のようだ。
とてつもないハイレグタイプだと思えば。しかし穴をどう捉えるが難しい。
お母さんが握ってくれたパンティー。
あの方程式を思いついてから最初に頭に浮かんだ素材。
申し分ない。
世界初のパンティー入りおでんが完成した。
ここまでやれば証明としてはもう十分だろう。 胸を張ってこの方程式は成り立つと言えるはずだ。
色の問題
形に関する問題は実践することで証明することが出来た。 しかしそれとは別に色に関する問題もある。
いままでは白い三角形にピンクのリボンというステレオタイプなもので やってきたが、白いブリーフを履く男性があまりいないように、一般的には三角形にもリボンにも様々な色が使われているはず。
そういった場合、方程式はどうなるのだろう。
いままでは白い三角形にピンクのリボンというステレオタイプなもので やってきたが、白いブリーフを履く男性があまりいないように、一般的には三角形にもリボンにも様々な色が使われているはず。
そういった場合、方程式はどうなるのだろう。
たとえば白い三角に白いリボンで考えよう。
白い三角に白いリボン、どちらも以前の方程式通りパンティーになっている。
問題は色を式にどう組み込むか。
私はそれを、分数にするという形で解決した。
問題は色を式にどう組み込むか。
私はそれを、分数にするという形で解決した。
この式を計算してみるとこうなる。
白い三角と白いリボンを足したら出来たのがツーホワイトパンティー。 かなり合点のいく方程式ではないだろうか。
ツーホワイトパンティーなおでん。
この式を先ほどまでの白い三角とピンクのリボンに適用してみよう。
なんということだろう。 パンティーが二つに増えてしまった。
いままで実際にやっていたが、出来たのは常に一つだった。 もう一つはどこか別の空間に出現していたのだろうか。
いままで実際にやっていたが、出来たのは常に一つだった。 もう一つはどこか別の空間に出現していたのだろうか。
この組み合わせだと、黄色いと黒のパンティーが作られることになる。
これの方程式は難しすぎてまだ人類には早すぎる。
いったん広告です
方程式に大きさは関係ない
色を式に入れると二つに増えるなど様々な問題が発生する。 なのでまだまだ検証すべきことは多いが、 色を考えなかった場合の方程式においては ほぼ確率されたといっていいだろう。
逆三角形にリボンを付ければどんなものでもパンティーになるというその方程式。 どんなサイズの物でも通用するのがそのすごさだ。
逆三角形にリボンを付ければどんなものでもパンティーになるというその方程式。 どんなサイズの物でも通用するのがそのすごさだ。
巨大な逆三角形といえば東京ビッグサイト。
透明な棒の先にリボンを付けた道具を用意する。
何万人も入る巨大なパンティーがここに誕生した。
横からの視点にも対応。
ビッグサイトの全ての面を使うと、全部で８つの巨大パンティーが出来る。
大きすぎていまいち見えない可能性もあるので、 より分かりやすい工夫を施してみよう。
収集したデータを一般向けに分かりやすくするのは大切なことだ。
これによりこの方程式がより強固に確証されたと言っていいだろう。 来年の試験の出題範囲に入ることが確実なのでぜひ覚えておこう。
とんでもないスケルトンタイプ。
